機率：生活當中充滿了許多的不一定，而這不一定大多伴隨著機率的存在，例如：擲骰子、投球、天氣、中獎、猜拳、實驗等，我們若想瞭解各個事件的機率就必須計算出其數值，然而這些數值常常是要經過繁瑣的過程，伴隨著變數與機率的不童也會增加計算的難易度。所以若能夠有效運用EXCEL中的運算功能便能夠輕鬆且準確地算出各項事件的機率。

在此假設做一實驗，共坐10次且每次的成功機率皆為0.6。則算出個別的機率為多少。
※備註：
次數---總實驗次數
成功機率---做一次實驗的成功機率
隨機變數X---成功次數
f(x)---當成功次數為x時的機率
F(x)---當成功次數為x時的累積機率

輸入個條件後按上方工具列中的<公式>--<其他函數>--<統計>--<BINOM.DIST>
NUMBER_S代表成功的次數也就是隨機變數X，故在框框內填$C2；TRIALS代表獨立實驗的次數，故輸入$A$2；PROBABILITY_S代表每次的成功機率，故輸入$B$2；CUMULATIVE若輸入0代表使用機率質量函數，輸入1則代表累績機率，故在此輸入0。按下確定後將綠色框框拖曳到整個D欄即可算出各值。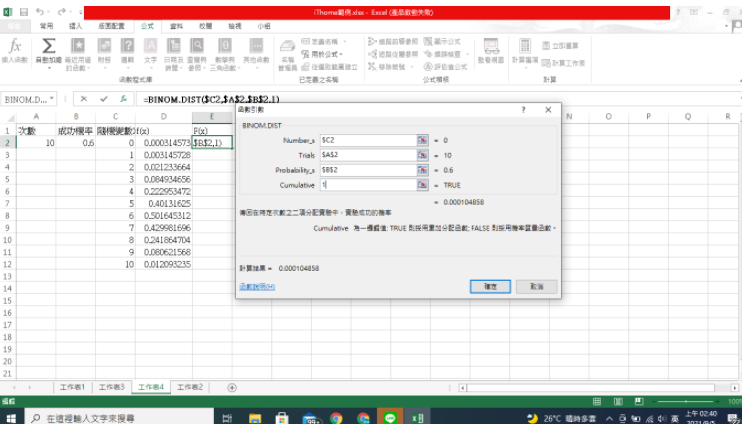

若要算出F(x)的值則方法同上，只要將CUMULATIVE的部分改為1即可算出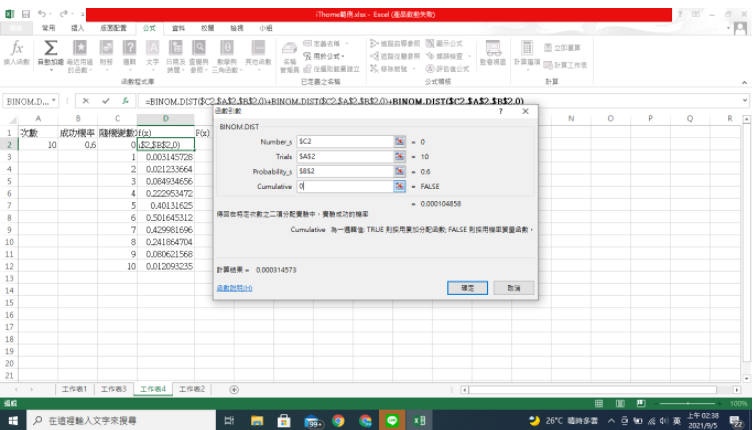

期望值即為次數＊成功機率---E(X)=np，故輸入=A2＊B2
變異數則為次數＊成功機率＊(1-成功機率)---Var(X)=npq，故輸入=A2＊B2＊(1-B2)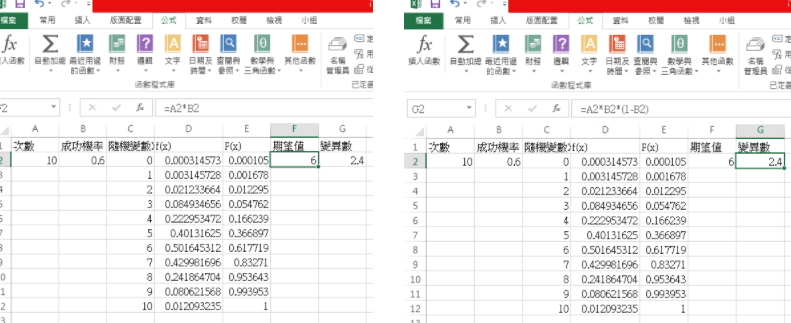

HYPERGEOMETRIC DISTRIBUTION
常用於不重複的抽樣事件
假設一個箱子內共擁有20顆球，其中有5顆為紅球，其餘為白球，若想知道隨機抽出三顆為紅球的個別機率值則：
輸入個數值後計算f(x)，點選工具列中的<公式>---<其他函數>---<統計>---<HYPGEOM.DIST>
當中sample_s即為隨機變數，故輸入=$D2；number_sample為抽取樣本數量，故輸入=$C$2；population_s為紅球數量，故輸入=$B$2；number_pop為求的總數量，及為紅球加白球的數量，故輸入=$A$2；cumulative如同上個例子，故輸入0，按下確定後將框框下拉至整個D欄為即可算出各數值。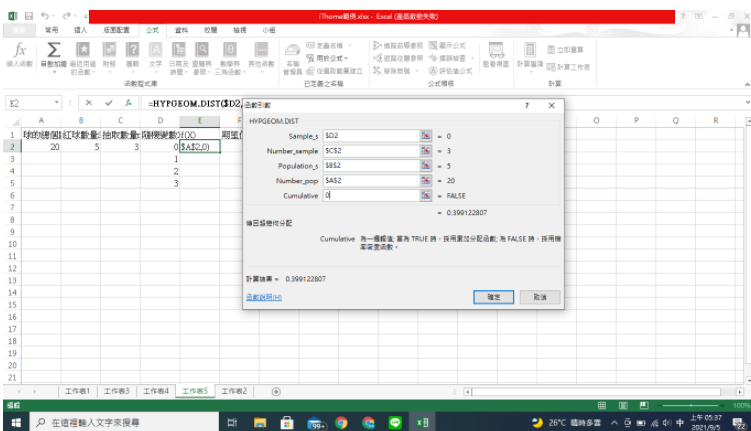

此時的期望值為E(X)=np，故在F2輸入=C2＊B2/A2
變異數為Var(X)=npq＊(N-n)/(N-1)，p=s/N、q=(N-s)/N，故在G2輸入=C2＊B2/A2＊(A2-B2)/A2＊(A2-C2)/(A2-1)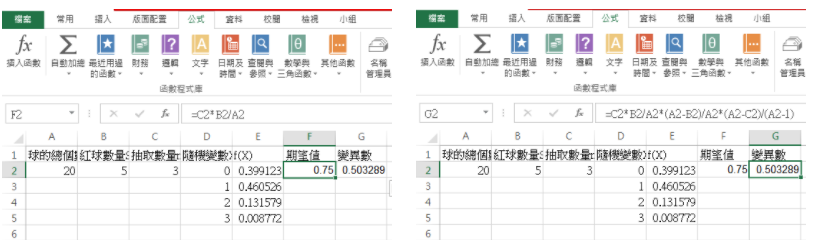

---20210919---